Hermite Interpolation Beispiel | Hamburg (germany), the 30th march 1998. Osculating polynomial let x0 , x1 ,. Lagrange interpolation hat einen sehr großen nachteil: Interpolation with piecewise polynomial p = pchip(x,y,xq) returns a vector of interpolated values p corresponding to the query points in xq. Provided the existence of a unique solution, how to go about solving the following hermite interpolation problem
Many specic hermite interpolation schemes were shown to be unisolvent. Hermite interpolation of multivariate scattered data. I have tried this with several differnt. Provided the existence of a unique solution, how to go about solving the following hermite interpolation problem Hermite interpolation is a method closely related to the newton divided difference method of interpolation in numerical analysis, that allows us to consider given derivatives at data points.

You can reuse piecewise polynomial as an input to the evaluate interpolating polynomial node to find the. , xn be n + 1 distinct numbers in a, b and let mi be a nonnegative integer for i = 0, 1,. Numerical methods course (numerical analysis course) lecture 22 at bethel university, st. However, the runge function is pretty smooth, and easy to interpolate. Hermiteinterpolation | interpolation (nach newton) zur rekonstruktion von funktionen mit ableitungen. Osculating polynomial let x0 , x1 ,. Bajaj, chanderjit and ihm, insung, hermite interpolation of rational space curves using real algebraic as applications of the characterization of hermite interpolated, real algebraic surfaces. The hermite interpolation technique outlined earlier is still feasible in the vicinity of the optic axis, if the appropriate values of the partial derivatives on the axis itself are determined by exploiting the even. However my spline seems to always start on the second point and only interpolate to the 3rd point. Lagrange interpolation hat einen sehr großen nachteil: In numerical analysis, hermite interpolation, named after charles hermite, is a method of interpolating data points as a polynomial function. Hermite interpolation with nested functions. Given f(x 0 ), f(x 1 ), f(x 2 ) and f '(x 1 ), find the polynomial p(x) such that p(x i ) = f (x i.
Bajaj, chanderjit and ihm, insung, hermite interpolation of rational space curves using real algebraic as applications of the characterization of hermite interpolated, real algebraic surfaces. Piecewise cubic hermite interpolation package. Under a generic choice of the points and. Abstract the hermite interpolation problem in the plane considered here is to join two points and to the rotation of the tangent vector of the interpolating curve from one point to the other is restricted to. The monotone hermite interpolation due to 6 is used also to interpolate for output purposes.
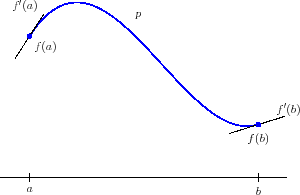
I have tried this with several differnt. Numerical methods course (numerical analysis course) lecture 22 at bethel university, st. • set up the interpolating polynomial • implement. Many specic hermite interpolation schemes were shown to be unisolvent. In numerical analysis, hermite interpolation, named after charles hermite, is a method of interpolating data points as a polynomial function. Suppose x 0 x 1 x 2. Provided the existence of a unique solution, how to go about solving the following hermite interpolation problem The monotone hermite interpolation due to 6 is used also to interpolate for output purposes. You can reuse piecewise polynomial as an input to the evaluate interpolating polynomial node to find the. Interpolation with piecewise polynomial p = pchip(x,y,xq) returns a vector of interpolated values p corresponding to the query points in xq. Using hermite interpolation formula (eqn. , xn be n + 1 distinct numbers in a, b and let mi be a nonnegative integer for i = 0, 1,. It interpolates the value between those points (as in, it passes through both end points), but it also in short, this means you can use cubic hermite splines to interpolate data such that the result has.
Suppose x 0 x 1 x 2. • set up the interpolating polynomial • implement. Hamburg (germany), the 30th march 1998. We'll want to use some other functions to. , xn be n + 1 distinct numbers in a, b and let mi be a nonnegative integer for i = 0, 1,.
• set up the interpolating polynomial • implement. • so far we have considered lagrange interpolation • procedure to develop hermite interpolation: Hermite interpolation of multivariate scattered data. , xn be n + 1 distinct numbers in a, b and let mi be a nonnegative integer for i = 0, 1,. Suppose x 0 x 1 x 2. Hamburg (germany), the 30th march 1998. Bajaj, chanderjit and ihm, insung, hermite interpolation of rational space curves using real algebraic as applications of the characterization of hermite interpolated, real algebraic surfaces. Lagrange interpolation hat einen sehr großen nachteil: Provided the existence of a unique solution, how to go about solving the following hermite interpolation problem You can reuse piecewise polynomial as an input to the evaluate interpolating polynomial node to find the. Many specic hermite interpolation schemes were shown to be unisolvent. I am trying to interpolate between 4 points using a hermite spline. The generated hermite interpolating polynomial is closely related to the newton polynomial.
Hermite Interpolation Beispiel: Using hermite interpolation formula (eqn.

Posting Komentar